序章
天文学と宇宙論
誰しもこの宇宙がなぜ存在するのか,またそもそも宇宙とはどのようなものなのかと疑問に思ったことがあるだろう.宇宙論 (Cosmology)はこの素朴な疑問を原動力として発展している研究分野である.科学が発展する以前にはこのような疑問は宗教的,哲学的対象であったため,宇宙に関しては推測に基づいたあいまいな描像しか得られていなかった.現代においては物理学などをもとにした科学的研究対象となり,科学技術の進歩に支えられて大きく発展している.
一方で,天文学(Astronomy) はもともと天体の運行などの現象を記述する現象論的なものであった.現代ではやはりさまざまな天体現象を物理学などをもとに記述する科学的研究対象となっている.古くからの天文学に対して,物理学に基づいて天体現象を研究する分野は天体物理学 (Astrophysics)とも呼ばれる.天文学の対象は星や太陽,惑星から始まり,銀河系,銀河団,超銀河団,宇宙の大規模構造へとその対象を広げてきた.これは科学技術の進歩によってより広い宇宙の姿を観測することができるようになってきたためである.宇宙の大きな構造が明らかになるにつれ,その構造をもたらした宇宙全体の振る舞いを定量的に研究できるようになり,宇宙論の研究も発展してきた.現在でも宇宙の観測はさらに広がりつつあり,大きな発見が相次いでいる.
宇宙論は,素粒子論や相対性理論などの基礎物理学の分野と有機的な結び付いて相互に発展するという面がある.現代宇宙論は時空を記述する基礎理論としての一般相対性理論,素粒子や原子の基本性質を記述する基礎理論としての素粒子論や原子核理論にその基盤を置いている.これら基礎物理学の分野は比較的古くから発展し,地球上で行える実験はほぼ理論的に説明可能な段階にまで達してきている.宇宙論的な問題に対してこれらの基礎理論を適用し,観測されているような宇宙の振る舞いを説明できるかどうかを調べることで,我々の得ている基礎理論が普遍的なものなのか,あるいは修正されてより基本的な理論に取って代わられるべきなのかを判定する手段ともなり得るのである.相対性理論の応用の場としての宇宙論は相対論的宇宙論(Relativistic cosmology)と呼ばれ,素粒子論の応用の場としての宇宙論は素粒子論的宇宙論と呼ばれる.これらの分野は基礎理論を宇宙論に応用するという面に重点があるが,逆に宇宙論的な観測をもとにしてこれら基礎理論を検証しようとする観測的宇宙論 (Observational cosmology)という分野がある.これらの各分野はもちろん独立したものではなく,相互に密接に関係して発展している.典型的な例として,宇宙のダークマター問題やダークエネルギー問題など,これまでの標準的な基礎理論では理解の困難な問題が観測的宇宙論によって提起され,基礎物理学全般に大きな影響を及ぼしている.
天文学的単位について
宇宙論で用いられる物理量のスケールは日常的なスケールとはかけ離れているため,通常物理で用いる単位を用いると文字どおり天文学的数字がいたるところに表れてしまい,あまり便利ではない.このため,通常天文学的スケールで定義された単位が用いられている.ここでは宇宙論で用いられる天文学的単位について説明しておく.ここでは数値はすべて有効数字4桁で表してある.より正確な数値は付録 A.2を参照せよ.
長さ
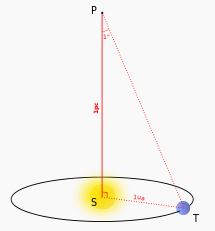
宇宙論で用いられる長さの単位はpc (パーセク, persec)である.これはもともと地球が太陽の回りを公転するときに星のみかけの位置がその星までの距離に応じて動いて見える現象を利用し,三角測量の原理によってその星までの距離を測るときに用いられた距離の単位である.一年間で地球が一回公転すると,星の見かけの位置は背景の十分遠い星々に対して移動するく.地球の公転面に垂直な方向にある星は円を描き,公転面上にある星は直線上を往復し,公転面からななめの方向にある星は一般に楕円形を描く.この楕円の長軸方向の角度は星までの距離に反比例する.この長半径の角度がちょうど1秒となるときの距離を 1pc と定義する.この距離は光が1年かかって進む距離,光年を単位にすると約3.26光年に対応し,メートルで表すと \(3.086\times 10^{16} \mathrm{m}\) に対応する.
左はパーセクの定義:Pは星の位置、Sは太陽の位置、Tは地球の位置。中は天の川銀河を正面に見る想像図:太陽系は銀河系の中心から8kpcの白抜きの星印のあたりと考えられる。右は乙女座銀河団で、中心が16.5Mpcの距離にあり1300以上の銀河を抱えている。
宇宙論に表れる距離はpcでもまだ小さすぎるため, \(10^{6}\mathrm{pc}\) を表すMpc (メガパーセク)がよく用いられる:
$$ \mathrm{Mpc} = 10^6 \mathrm{pc} = 3.086 \times 10^{22} \mathrm{m} \tag{A.2.1}$$
この他にもキロパーセク \(\mathrm{kpc} = 10^3 \mathrm{pc}\) , ギガパーセク \(\mathrm{Gpc} = 10^9 \mathrm{pc}\) も使われる.現在我々に観測可能な宇宙の半径の目安は約 \(4 \mathrm{Gpc}\) である.
時間
宇宙論においては初期の宇宙では現象の進行がかなり速く,後期になるにつれ非常に遅くなっていくので,秒 (s),分 (min),時 (hr),日 (day), 年 (yr) などが状況に応じていずれも用いられる.比較的現在の宇宙年齢を表すのに良く使われるのは10億年を表す Gyr (ギガイヤー)である.これは秒 (s)で表すと,
$$ \mathrm{Gyr} = 3.156 \times 10^{16} \mathrm{s} \tag{A.2.2}$$
である.現在の宇宙の年齢は約 \(14 \mathrm{Gyr}\) である.
質量
銀河や銀河団など,宇宙の構造に対する質量の単位として通常用いられるのは太陽質量\(M_\odot\) である.これは,kgで表すと
$$ M_\odot = 1.988 \times 10^{30} \mathrm{kg} \tag{A.2.3}$$
となる.
星の宇宙から銀河宇宙へ
この世界が全体としてどういうものであるのかは,人間の抱くもっとも基本的な疑問といえるだろう.これを知るために最も適切な方法は,できる限り宇宙を広く観測することである.星から銀河の宇宙へ発展してきた歴史を振り返ると、
ハーシェル (William Herschel)
天の川は銀河系である. \(\Leftarrow\) 星の数のカウント (1785-89年)
太陽を中心とした円盤形をした銀河系の描像 \(\Rightarrow\) カプスタイン宇宙(1922)
シャプレー (Harlow Shapley)
セファイド変光星 (Cepheid variables, Cepheids) を用いた距離決定 \(\Rightarrow\) 太陽は銀河系の中心ではない描像
シャプレーとカーチス (H. D. Curtis)の“大論争” [The Great Debate, 1920年4月26日 ]
シャプレー:天の川の大きさは100kpc程度,そのまわりにずっと小さな渦巻星雲が取り囲む説
カーチス:天の川の大きさは10kpc程度,渦巻星雲は天の川と同等の銀河であるという説
カーチスは銀河系の大きさについては小さく見積もり過ぎていたが、「渦巻き銀河は銀河系の外にある独立した銀河である」とした点で正しかったことが、後のハッブルの観測で判った。
ハッブル (Edwin Hubble)
1923年,渦巻星雲 M31 (アンドロメダ星雲)および M33 にセファイド変光星を発見.距離を見積もると約300kpc !! \(\Rightarrow\) 渦巻星雲は別の銀河系である!
ウイリアム・ハーシェル、ハーロー・シャプレー、エドウィン・ハッブルの写真 (Wikipediaから)
銀河のタイプ
銀河は、その形状で分類で、おおまかにハッブルの音叉図 (Huble's Tuning Folk Diagram)あるいは、ハッブル・ダイヤグラム(Hubble Diagram)と呼ばれるもので分類される。
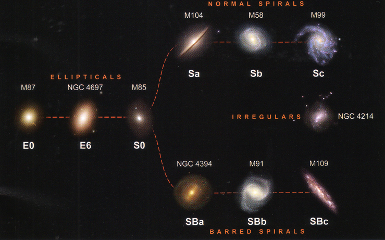
ハッブル・ダイヤグラム:銀河を形状で分類するもので、楕円銀河(Ellipticals)、渦巻銀河(Normal Spirals)、棒渦巻銀河(Barred Spirals)の3つの分岐からなるが、
どれにも分類できないものは不規則銀河(Irregulars)と呼ばれる。分類番号の上に、典型的な例が、カタログ番号で書かれている。
楕円銀河(E)
E0: 球状の楕円銀河 \(\Rightarrow\) E3:楕円率0.3の楕円銀河 \(\Rightarrow\) E7:楕円率 0.7の楕円銀河
渦巻銀河(S)
S0:レンズ状銀河 \(\Rightarrow\) 渦巻きが見え、そのほどけ具合で分類:Sa 渦が密に巻きついている \(\Rightarrow\) Sc 渦がほどけて広がっている
棒状渦巻銀河(SB)
S0:レンズ状銀河 \(\Rightarrow\) 中心に棒状の構造が見え、その外に渦巻きが見え、そのほどけ具合で分類:SBa 渦が密に巻きついている \(\Rightarrow\) SBc 渦がほどけて広がっている
不規則銀河(Irregulars)
上の3つの分類に入らない、不規則な形をした銀河も多くある。それらをまとめて、不規則銀河と呼ぶ。
他にも分類法はいくつかあるが,いまだに完全な定量的な分類法は確立していない.銀河には一般に多様な個性がある。
クェーサー
クェーサー(Quasar)の歴史は、1960年に、強い電波を出す銀河、3C273や3C48の中心部に、明るい点光源が発見され、正体が判らないまま、Quasi-Stellar Radio Source (準恒星状電波源) と呼ばれたことに始まる。その後、電波源でない同様の天体もクェーサーと呼ばれるようになり、名前が不適切になったが、この名前は使われ続けている。QSO (Quasi-stellar Object) 呼ばれることが多い。
宇宙の膨張
宇宙が膨張していることが確立されてきた歴史を振り返る。
1912-1925 V. M. Slipher
銀河のスペクトルはほとんど赤方偏移をしている.青方偏移をするものはごくわずか。
1929 E. Hubble
銀河の遠ざかるスピード \(\propto\) 距離 [Hubble, Edwin 1929] $$ v = H_0 r \tag{A.6.4}$$
\(H_0\) :ハッブル定数 (Hubble's constant)。現在の見積もりでは、$$ H_0 = 70 {\rm km/s/Mpc} \pm 10\% \tag{A.6.5}$$
ハッブル定数の不定性を\(\Delta h\) によりあらわす:$$ H_0 = 100 h {\rm km/s/Mpc} \tag{A.6.6}$$
このとき、\(\Delta h =0.7 \pm 10\%\) 。\(H_0 \sim 530 {\rm km/s/Mpc}\) という大きなものだった。\(r/v = {H_0}^{-1}\) である。これをハッブル時間 (Hubble time) という:$$ {H_0}^{-1} = 9.78 \times 10^9 h^{-1} {\rm yr} = 9.78 h^{-1} {\rm Gyr} \tag{A.6.7}$$
また,ハッブル時間あたりに光の進める範囲 \(c{H_0}^{-1}\) は現在の宇宙が因果関係を持てる範囲をおおっざっぱに表し、これをハッブル距離(Hubble distance)あるいは、ハッブル半径(Hubble radius)という:$$ c {H_0}^{-1} = 2998 {\hbox {$h^{-1}$}{\rm Mpc}} \tag{A.6.8}$$
宇宙の大規模構造
銀河の空間的な分布は一様なわけではない。かなり大きなスケールまで構造がある。これは、宇宙の大規模構造と呼ばれる。
銀河群 (groups of galaxies)
数個~数十個の銀河の集まり \(\lower.5ex\hbox{$\; \buildrel < \over \sim \;$}1 {\hbox {$h^{-1}$}{\rm Mpc}} \)
銀河団 (clusters of galaxies)
数百-千個の銀河の集まり \(\sim 5 {\hbox {$h^{-1}$}{\rm Mpc}} \)
超銀河団 (superclusters)
数千個の銀河の集まり \(\lower.5ex\hbox{$\; \buildrel > \over \sim \;$}50 {\hbox {$h^{-1}$}{\rm Mpc}} \)
ボイド領域 (voids)
銀河のほとんどない領域 \(\sim$ 100-200 $ {\hbox {$h^{-1}$}{\rm Mpc}} \)
フィラメント構造 (filaments)
ボイド間にある細長く連なる銀河分布。超銀河団にかかる橋のような構造。
セル構造 (cell-structure)
約 \(125 {\hbox {$h^{-1}$}{\rm Mpc}} \) のセル状の構造?
宇宙の背景放射
背景放射(background radiation)と呼ばれる、光源が特定できない、宇宙全体に広がった放射がマイクロ波の領域で、ペンジアスとウイルソンによって、発見された。[Penzius&Wilson 1965]
ほぼ完全な黒体放射であり、温度はほぼ2.7度である。
太陽系の局所的な運動で生じることが判っている、双極子成分を除けば、\(10^{-5}\) の精度で等方的である。
マイクロ波背景放射は、ビッグバンの名残として、いろいろな宇宙論に関するモデルを検証する上で、極めて重要な情報源となっている。
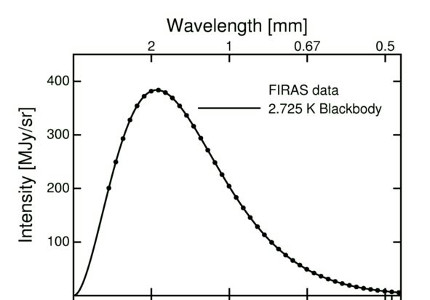
NASAのCOBE衛星に搭載されたFIRAS観測器が観測した、宇宙マイクロ波背景放射のスペクトル。黒体放射と仮定してフィットすると、2.725度で、非常に良く再現できる。(UCLAのWright教授のウェブページから)
ダークマターとダークエネルギー
ダークマター(暗黒物質、Dark matter)は、フリッツ・ツビッキー(Fritz Zwicky)が、かみのけ座(Coma cluster)の質量を、「明るさ」から推測する従来方法と、銀河の速度分散からビリアル定理を使って推測する方法で求め比較した、1934年の論文で導入された。ツウィっキーは、その結果「暗黒物質("dunkel Materie")が明るい物質("leuchtende Materie")よりも、はるかに高い密度で存在すると言う、驚くべき結論に至る」と書いている。[Zwicky 1934年論文]
銀河内の星間ガスの回転速度分布
銀河団による、背景銀河の重力による「歪み」(重力レンズ効果)
2つの銀河団の衝突で見られるダークマターと明るいガスの分離現象
ダークエネルギー(Dark Energy)の導入は、1998年に発表された、遠方銀河で発生したIa型と呼ばれる超新星の明るさと赤方偏移(宇宙膨張により地球から遠ざかる後退速度と関係)の観測結果の発表に由来する[Perlmutter他の論文、Riess他の論文] 。観測結果は、当時の標準的な宇宙論の予想より速く遠ざかっていることを示していた。宇宙空間には、宇宙を膨張させる「斥力(せきりょく)」があると解釈され、この斥力の源がダークエネルギーと呼ばれるようになった。その後、ダークエネルギーの存在は、宇宙背景放射の観測などでも確立されているが、その正体は未だ解明されていない。
WMAP衛星やPlanck衛星による、宇宙背景放射のスペクトル観測などから、宇宙のエネルギー密度に換算すると、全体の約74%を占めていることが判っている。
ダークエネルギーの解釈には、アインシュタインが一般相対論で導入した「宇宙定数」とする考えと、未知の力に起因する考えの、2つの流れに分類できる。
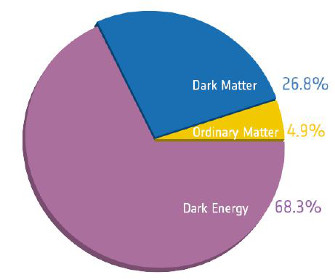
ヨーロッパ宇宙機関(ESA)のPlanck衛星が観測した宇宙背景放射のスペクトルを、最新の宇宙論モデル(ラムダCDMモデルと呼ばれ、\(\Lambda\) CDMやLCDMと略記される)を仮定して求めた宇宙のエネルギーの成分比。ダークエネルギー(Dark Energy)がもっとも大きな割合(68.3%)で、ダークマター(Dark Matter)が次に大きく(26.8%)、我々の周りにある通常の物質(Ordinary Matter)は4.9%に過ぎない[Planck 2015年の結果] 。ちなみに、現在の観測精度ではダークエネルギーと宇宙項(\(\Lambda\) ラムダ)の区別できないため、「ラムダ」は2つの可能性の総称となっている。またCDMは、Cold Dark Matterの略で、運動速度が低い(低温)のダークマターの意味である。
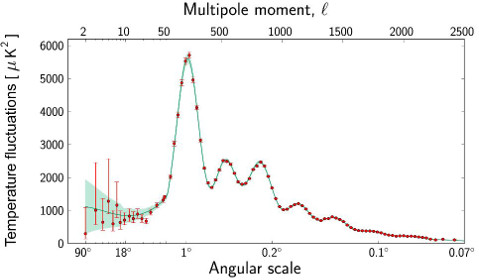
左:Planck衛星が観測した、宇宙マイクロ波背景放射のスペクトルから決められた、宇宙のエネルギー成分比。Univ. College Londonの宇宙論グループのダークエネルギー解説記事 右:WMAP衛星が観測した一定角度離れた点のマイクロ波の温度の相関を、全天で平均し、分離角あるいは多重極モーメントでプロットしたもの。Planck衛星では、より高い精度で測られた。ESAのPlanck衛星で得られた画像アーカイブより
序章の文献
Wikipedia https://en.wikipedia.org/wiki/Great_Debate_(astronomy)
Hubble, Edwin (1929): “A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae”. Proceedings of the National Academy of Sciences of the United States of America 15 (3): 168-173. doi:10.1073/pnas.15.3.168.
A. A. Penzias and R. W. Wilson, "A Measurement of Excess Antenna Temperature at 4080 Mc/s," Astrophysics Journal 142 (1965), 419.
Zwicky, F. (1933). “Die Rotverschiebung von extragalaktischen Nebeln”. Helvetica Physica Acta 6: 110–127.
Perlmutter, S., et al., "Discovery of a Supernova Explosion at Half the Age of the Universe and its Cosmological Implications" Nature, 1 January 1998
Planck Collaboration, P. Ade et al., "Planck 2015 results. XIII. Cosmological parameters" Astronomy & Astrophysics (to appear), http://adsabs.harvard.edu/abs/2015arXiv150201589P
ロバートソン・ウォーカー計量
アインシュタインの一般相対論は(1915,1916)、それ以前から観測では確立しながら理論的に謎であった「水星の近日点移動」を正確に算出し、太陽が恒星の近傍に来ると位置がずれて見えると予言が観測で確認されると(アーサー・エッディントン 1919年)、多くの物理学者が、一般相対論で宇宙を記述しようと考えるようになった。、その際、一般相対論では、絶対座標や絶対時間が定義できず、構成要素である星や原子、さらには宇宙線がランダムに飛び交う軌道で個々に定義されることが問題となった。までを記述しようとしても,あまりに複雑すぎて理論的な定式化は不可能である。そのような理論があるとすると、宇宙のふるまいと同時に、昨日食べた夕食をも正確に記述するようなものを目指すことになる。だが,ここでは夕食のことはひとまず忘れて、巨視的な宇宙に想いを馳せることにしよう。そのためにまず宇宙を大きく近似することにより簡単化して扱うことを考える。その後、必要に応じて,より細かな記述が可能となるよう、近似を上げていくことになる。
ワイルの要請(仮説)(Weyl's Postulate)
宇宙の時空のふるまいは一般相対論によって調べられるが、そのためには宇宙に、時間と空間の座標(時空の座標)を張りわたす必要がある。一般相対論では、絶対座標はなく、構成する粒子や星が時空の中で描く軌跡(世界線と呼ぶ)に沿って各々異なる時間が決まることになる。こうなると宇宙では厳密な意味で、宇宙の時間座標を定義することができない。ここでヘルマン・ワイル(Herman Weyle)は、世界線を流体の流れに喩えて、「世界線は、互いに束のように集まって、過去から未来へ流れ広がって行く」との仮説を提唱した[Herman Weyl(1923)]。
物質の世界線はお互いに交差しない測地線の束をなし、これらの測地線は一連の空間的3次元超面(hypersurface)に垂直である.これをワイルの要請、あるいは仮説(Weyl's postulate)と呼ぶ。
ただし,後に明らかになるように,宇宙の初期には密度が無限大になる特異点が予想されるが,その点ではすべての世界線が一点に集約する。このような初期の特異点のみは上の要請の例外とする。
ワイルの要請のもとでは、粒子や星などの物質素片ごとに空間座標 \(x^i\) (\(i=1,2,3\) )、3次元超面ごとに時間座標 \(x^0\) (\(x^0=ct\) ) を張ることができ,これらが時空を記述する座標系、\(x^\mu\) (\(\mu = 0,1,2,3\) ) を構成する。ここで交差する世界線があると1点に2つの\(x^\mu\) の値が対応してしまってこのような座標は張ることができなくなるため,ワイルの要請が本質的である。世界線を流体の流線と考えると、理解し易い。
このときにワイルの要請を満たす宇宙の計量を求めよう。まず、測地線の接ベクトル、\((n^\mu)=(1,0,0,0)\) と3次元超面上の任意の接ベクトル、\((\sigma^\mu)=(0,\sigma^i)\) が垂直になることから、
$$ n^\mu \sigma_\mu = g_{0i}\,\sigma^i = 0 \tag{B.1.1}$$
であるが、ここで\(\sigma^i\) は任意なので、結局
$$ g_{0i} = 0 \tag{B.1.2}$$
が要請される。一般にブロック対角形の行列の逆行列も同様にブロック対角形なので,
$$ g^{0i} = 0 \tag{B.1.3}$$
でもある。
座標値一定 \(x^i = {\rm const}\) の点が測地線をなす座標では、測地線方程式
$$ \frac{d^2 x^\mu}{ds^2} + {\mit\Gamma}^\mu_{\nu\lambda} \frac{dx^\nu}{ds}\frac{dx^\lambda}{ds} = 0 \tag{B.1.4} $$
の\(\mu = i\) 成分は
$$ {\mit\Gamma}^i_{00} \left(\frac{dx^0}{ds}\right)^2 = 0 \tag{B.1.5} $$
となる。ここで、\(dx^0/ds\) は時間座標と物質素片の固有時間との比であるからゼロにはならず、結局 \({\mit\Gamma}^i_{00} = 0\) である。クリストッフェル記号は
$$ {\mit\Gamma}^\mu_{\nu\lambda} = \frac12 g^{\mu\sigma} \left( g_{\sigma\nu,\lambda} + g_{\sigma\lambda,\nu} - g_{\nu\lambda,\sigma} \right) \tag{B.1.6}$$
であるから、この条件は
$$ g^{i\sigma} g_{00,\sigma} = 2 g^{i\sigma} g_{0\sigma,0} \tag{B.1.7}$$
となる。これは、条件(2.1.2)、(2.1.3)により、
$$ \frac{\partial g_{00}}{\partial x^i} = 0 \tag{B.1.8}$$
と同値である。
計算を進めてゆくと、\(g_{00}\) は\(x^0\) のみの関数であることがわかる。したがって、\(x^0\) を、
$$ dx^0 \rightarrow \frac{dx^0}{\sqrt{- g_{00}(x^0)}} \tag{B.1.9}$$
のように定義し直すといつでも\(g_{00}=-1\) とすることができることになる。
まとめると、ワイルの要請を満たす計量として次の形式で記述できる座標が常に取れることになる:
$$ ds^2 = - (dx^0)^2 + g_{ij} dx^i dx^j \tag{B.1.10}$$
$$ = - c^2 dt^2 + g_{ij} dx^i dx^j \tag{B.1.11}$$
このとき\(t=x^0/c\) を宇宙時間(cosmic time)と呼ぶ。これが物質素片の固有時間となっていることは,式(B.1.10)で \(x^i={\rm const.}\) の世界線を考えれば明らかであろう。また、ワイルの要請における3次元超面は宇宙時間一定の面である。
宇宙原理(Cosmological Principle)
次に宇宙原理と呼ばれるものを導入する.これは次の仮定である:
もちろん、小さなスケールでは宇宙は一様でも等方でもないことは明らかであるが,大きなスケールでは宇宙のどの場所にも特別な場所や方向はないと考えられる。
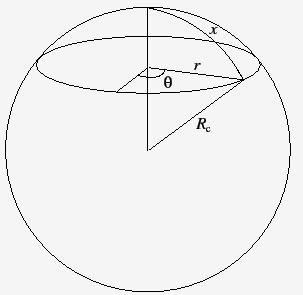
宇宙原理を満たす計量を考えるのには、まず2次元空間について考えるとわかりやすい。球の表面は曲率が正の一様等方な2次元面をなす。球の半径を \(R_{\rm c}\) とするとき、曲率は \(K \equiv {R_{\rm c}}^{-2}\) で定義される。球の北極点を球面上の原点Oとして,適当な方向からの角度\(\theta\) と原点からの測地的距離\(x\) によって2次元極座標を張ることができる。このとき、点 \((x,\theta)\) からOと球の中心を結ぶ直線上へ降ろした垂線の距離を \(r\) とすれば、 \(r = R_{\rm c} \sin(x/R_{\rm c})\) である (図B.2.1)。
球面の幾何学:経度と経線に沿った原点からの距離で、場所が決まる。
したがって、球面上の2次元線素は次の形となることがわかる:
$$ dl^2 = dx^2 + r^2 d\theta^2 \tag{B.2.12}$$
$$ = \frac{dr^2}{1 - K r^2} + r^2 d\theta^2 \tag{B.2.13}$$
これが2次元正定曲率空間の計量である。球の場合は\(R_{\rm c}\) が正の実数であるから\(K>0\) であるが、この計量は\(K \leq 0\) に解析接続することができ、\(K=0\) のときは平面の極座標の計量に、また\(K < 0\) のときは定負曲率空間の計量になる。
この2次元の定曲率空間の計量を足がかりにして3次元定曲率空間の計量が構成できる。まず、3次元空間の中に任意に原点をとって極座標 \((r,\theta,\phi)\) を張って、その線素を \(dl^2 = \gamma_{ij} dx^i dx^j\) とする。等方性より動径座標\(r\) が一定の面は一様な球面を構成する。さらに、動径方向の座標として、この球面の面積が\(4\pi r^2\) となるようにとることにしよう。この座標は 2次元の場合同様、空間が曲がっている場合には実際の距離とは異なるが、計量としては簡単な形となる。こうして、この球面上の線素は \(r^2(d\theta^2 + \sin^2\theta d\phi^2)\) となる。また、動径方向と角座標 \(\theta,\phi\) 方向は垂直である。そうでなければ動径方向の角度方向への射影が非等方性を生むことになってしまう。したがって \(\gamma_{r\theta} = \gamma_{r\phi} = 0\) でなければならない。以上により、空間の等方性により計量として次の形に制限できることがわかる:
$$ dl^2 = h(r) dr^2 + r^2 \left(d\theta^2 + \sin^2\theta d\phi^2\right) \tag{B.2.14}$$
ここで、\(h(r)\) は任意関数であり、等方性の条件からは決まらないが、一様性の条件から一意的に定まる。すなわち、\(\phi = {\rm const.}\) の面を考えてみると、対称性によってこれは一様等方2次元空間をなすので、計量 (2.2.14)が(2.2.13)に帰着するような座標が存在すると考えられる。このことから \(h(r) = 1/(1 - K r^2)\) と決めることができる。したがって宇宙原理を満たす3次元計量は最終的に$$ dl^2 = \frac{dr^2}{1 - K r^2} + r^2 \left(d\theta^2 + \sin^2\theta d\phi^2\right) \tag{B.2.15}$$
であることがわかる。
座標変換の自由度を別にすればこの計量以外には一様等方性を満たす計量はない。これを見るには、3次元の曲率テンソル \({}^{(3)}R_{ijkl}\) の形が一様等方性からどのようなものでなければならないかを考えるとよい。空間に特別な方向がないことから、これは3次元計量テンソル \(\gamma_{ij}\) のみを用いて表されなければならない。もし何らかの他のベクトルやテンソルで表せるとすると、そのベクトルやテンソルが空間に特別な方向を定義してしまうからである。すると、曲率テンソルの添字の対称性(B.2.63)-(B.2.66)を満たすものとしては、次のものしかない:
$$ {}^{(3)}R_{ijkl} = K\left(\gamma_{ik}\gamma_{jl} - \gamma_{il}\gamma_{jk}\right) \tag{B.2.16}$$
この形から3次元スカラー曲率は \({}^{(3)}R = 6K\) であるが、空間の一様性から、これは定数でなければならない。したがって、一様等方性を満たす計量は一つの定数\(K\) により表されるものしかないことがわかる。この\(K\) が上で導いた計量(2.2.15)の曲率\(K\) と同一のものであることは計量から直接スカラー曲率を計算してみると\(6K\) に一致することからわかる。
上の計量(2.2.15)において、曲率\(K\) がゼロでなければ、原点からの測地的距離は \(r\) ではないことは2次元の例からも明らかであろう。動径座標\(r\) 一定の面の面積は \(4\pi r^2\) となるが、これは曲率がゼロのときのみ \(r\) が実際の測地的距離となることを示している。ゼロでない曲率が存在する場合は、動径座標一定の球面の面積が \(4\pi r^2\) となるように動径座標を定義したことになる。
ロバートソン・ウォーカー計量(Robertson-Walker Metric)
空間の計量は一様等方空間の場合、時間に依存する定数倍を除いて、式(2.2.15)により決まってしまうので、ワイルの要請と宇宙原理を同時に満たす計量は
$$ ds^2 = -c^2 dt^2 + a^2(t) \left[ \frac{dr^2}{1 - K r^2} + r^2 \left(d\theta^2 + \sin^2\theta d\phi^2\right) \right] \tag{B.3.17}$$
となる。これをロバートソン・ウォーカー計量 (Robertson-Walker Metric:RW計量)と呼ぶが、歴史的には、Friedmannがアインシュタイン方程式の解として発見し、Lemaître、Robertson、Walkerが発展させたので、FLRW計量と呼ばれることもある[Wikipedia] 。この計量は宇宙論において最も重要なものの一つである。空間のスケールを決める \(a(t)\) はスケール因子(scale factor)というもので、空間の膨張や収縮を表わすことになる。また、曲率\(K\) は一般に時間変化をしてもよいが、その場合でも動径座標 \(r\) の再定義をすれば結局スケール因子の時間変化にくりこまれるので、一般性を失なわずに \(K\) は定数であるとしてよい。このときの定数として、現在時刻 \(t=t_0\) の曲率を採用すれば、現在時刻でのスケール因子は \(a(t_0) = 1\) という規格化をもつことになる。以下ではこの規格化を用いることとする。
上の形は球面の面積で定義される動径座標 \(r\) によって表示されるものであるが、動径座標の定義を変えることにより、他の形にも書き表わすことができる。まず、次の変数変換
$$ \bar{r} = \frac{2r}{1 + \sqrt{1 - K r^2}} \tag{B.3.18}$$
により,ロバートソン・ウォーカー計量は
$$ ds^2 = -c^2 dt^2 + \frac{a^2(t)}{\left(1 + \frac{K}{4}\bar{r}^2\right)}\left[d\bar{r}^2 + \bar{r}^2 \left(d\theta^2 + \sin^2\theta d\phi^2 \right)\right] \tag{B.3.19}$$
という形となる。この形から、RW計量は共形変換 (conformal transformation) \(g_{\mu\nu}(x) \rightarrow \Omega(x)g_{\mu\nu}(x)\) により平坦な空間の計量と同じ形となるという性質を持っていることがわかる。
スケール因子が \(a=1\) のとき、実際の測地的距離 \(x\) は動径座標 \(r\) と
$$ dx = \frac{dr}{\sqrt{1 - K r^2}} \tag{B.3.20}$$
の関係にあるので、これを積分して得られる関数を \(r = {S_K}(x)\) とすると
$$ {S_K}(x) = \left\{
\begin{array}{ll}
\frac{\rm sinh(\sqrt{-K}x)}{\sqrt{-K}} & (K < 0) \\
x & (K = 0) \\
\frac{\rm sin(\sqrt{K} x)}{\sqrt{K}} & (K > 0) \end{array} \right. \tag{B.3.21}$$
である。上の規格化ではこれは現在の宇宙での測地的距離を表している。したがってRW計量は
$$ ds^2 = -c^2 dt^2 + a^2(t) \left[ dx^2 + {S_K}^2(x) \left(d\theta^2 + \sin^2\theta d\phi^2\right) \right] \tag{B.3.22}$$
という形にも表わすことができる。物質素片に固定された点は、原点からの測地的距離がスケール因子に比例して増えていく。この座標 \(x\) は \(a=1\) となるときの、実際の測地的距離である。これを共動距離(comoving distance)という。
さて、上で採用した \(a(t_0) = 1\) とは異なる規格化もまた広く使われることがあるので、ここでコメントしておく。曲率がゼロでないとき、座標 \(r\) に曲率 \(K\) の値による再定義 \(r \rightarrow \vert K\vert^{-1/2} r\) を行なえば、
$$ ds^2 = -c^2 dt^2 + R^2(t) \left[ \frac{dr^2}{1 - k r^2} + r^2 \left(d\theta^2 + \sin^2\theta d\phi^2\right) \right] \tag{B.3.23}$$
となる。ここで、
$$ k = \left\{
\begin{array}{ll}
-1 & (K < 0) \\
0 & (K = 0) \\
1 & (K>0)
\end{array} \right.
\hskip 50pt
R(t) = \left\{ \begin{array}{l} \vert K\vert^{-1/2} a(t) & (K
\neq 0) \\ a(t) & (K = 0) \end{array} \right. \tag{B.3.24}$$
である。曲率がゼロでない場合には \(r\) は無次元化していて、曲率は離散的な値、\(0,\pm 1\) のみをとる。さらにスケール因子 \(R(t)\) は長さの次元を持つ。したがって単位系を再定義しない限り現在値を \(1\) に規格化することができない。それは \(R(t_0) = \vert K\vert^{-1/2}\) となり、曲率のスケールはスケール因子の現在値を通して入ってくることになる。このような規格化を用いる場合には注意すべき事項である。
赤方偏移(Red Shift)
ある点を出た光が観測者に届くとき、その波長は宇宙のスケール因子の変化を感じて変化する。このことを定量的に見てみる。そのために、観測者は原点 \(r=0\) にいて、時刻 \(t=t_1\) に点 \((r_1,\theta_1,\phi_1)\) を出た光を、現在時刻\(t=t_0\) に観測するものとする。光線は原点までヌル測地線 \(ds = 0\) に沿って到達する。空間の等方性により光線は \(d\theta = d\phi = 0\) を満たしながら進むので、RW計量により、
$$ c dt = \pm \frac{a(t) dr}{\sqrt{1 - K r^2}} \tag{B.4.25}$$
となる。座標値が減少する方向に光線が進むので、符号はマイナスをとることになり、光線に沿って積分すれば、
$$ \int_{t_1}^{t_0}\frac{c dt}{a(t)} =
\int_0^{r_1} \frac{dr}{\sqrt{1 - K r^2}}
\tag{B.4.26}$$
となる。
いま、波の山が時刻\(t_1\) に出発し、次の波の山が時刻 \(t_1 + \delta t_1\) に出発したとする。そして、初めの山の到達時刻を \(t_0\) 、次の山の到達時刻を \(t_0 + \delta t_0\) とする。ここで、式(2.4.26)の右辺は時間に依存しないことに注意しよう。すると、
$$ \int_{t_1}^{t_0}\frac{dt}{a(t)} =
\int_{t_1+\delta t_1}^{t_0+\delta t_0} \frac{dt}{a(t)} \tag{B.4.27}$$
が成り立つ。ここで、\(\delta t_0\) 、\(\delta t_1\) はスケール因子の時間変化のスケールに比べて十分短かいと考えられるので、式(2.4.27)をテイラー展開することにより、$$ \frac{\delta t_1}{a(t_1)} = \frac{\delta t_0}{a(t_0)} \tag{B.4.28}$$
となる.光の波長は光源と観測者でそれぞれ \(\lambda_1 = c \delta t_1\) , \(\lambda_0 = c \delta t_0\) である.ここで,赤方偏移\(z\) を波長の伸び具合を表わす量として, \(1 + z \equiv \lambda_0/\lambda_1\) で定義する.すると, \(a(t_0) = 1\) の規格化のもとで、
$$ 1 + z = \frac{1}{a(t_1)} \tag{B.4.29}$$
となることがわかる。膨張宇宙では過去から来た光は \(a(t_1) < 1\) を満たすので,赤方偏移 \(z\) は必ず正となる。
ここで、初等的な解説ではよく説明の平易さのために、赤方偏移をドップラー効果によって説明する場合があるが、これについてコメントしておく。宇宙膨張を空間の膨張ではなく、単に物質の膨張運動により解釈するニュートン的宇宙論を採用したときには、ドップラー効果と考えることに問題はない。だが、上の導出から明らかなように、膨張宇宙における赤方偏移は、光の伝播の途中で空間の膨張にひきずられて波長が長くなることによるものである。これは、ドップラー効果とは厳密には異なる概念である。ドップラー効果は光の放射時点で光源と観測者との速度差がはっきりしている場合に初めて曖昧さなく定義できる物理的効果である。一方、一般相対論では、異なる場所での速度差の自然な定義が存在しない。したがって、膨張宇宙の赤方偏移がドップラー効果であるという言明には、物理的な曖昧さがある。光の進路に沿っての無限小のローレンツ変換の積み重ねによるドップラー効果と解釈することも不可能ではないが、不自然であり、あくまでドップラー効果による理解は初等的な説明の平易さのためのものであると思っておいたほうがよいであろう。一様等方な宇宙に対して運動しているような光源から出る光には,真の意味でのドップラー効果による波長の変化が、宇宙膨張による赤方偏移とは別に加わることになる。
見かけの明るさ(Apparent Brightness)
光の伝播の途中で吸収がない理想的な場合、天体そのものの光度(luminosity) \(L\) と我々が観測する見かけの天体の明るさ \(F\) は比例する。ここで、\(L\) は天体の静止系において単位時間あたりに放出される全エネルギーであり、\(F\) は単位面積、単位時間あたりに観測者が受けるエネルギーであり、これを観測者の位置でのフラックス (flux) という。静止ユークリッド空間での関係は
$$ F = \frac{L}{4 \pi r^2} \tag{B.5.30}$$
であるが、RW計量では膨張と曲率の効果により、この関係は変更を受ける。
まず、赤方偏移によって光のエネルギーが小さくなる。そこで、光源において波長範囲 \(\lambda \sim \lambda + d\lambda\) の中に放出されるエネルギーを \(L\cdot I(\lambda) d\lambda\) とする。ここで、\(L\) は全放出エネルギーであり、\(I(\lambda)\) はエネルギー分布を表す関数で、規格化
$$ \int_0^\infty I(\lambda) d\lambda = 1 \tag{B.5.31}$$
を持つ。光源から、波長範囲 \(\lambda \sim \lambda + \Delta\lambda\) 、時間範囲 \(t \sim t + \Delta t\) の間に放出されるエネルギーは
$$ \Delta E = L\cdot I(\lambda)\Delta\lambda \Delta t \tag{B.5.32}$$
である。1光子あたりのエネルギーは \(2\pi\hbar c/\lambda\) であるから、その光子数は
$$ \Delta N = \frac{\Delta E}{2\pi\hbar c/\lambda} = \frac{L}{2\pi\hbar c} \lambda I(\lambda) \Delta\lambda \Delta t \tag{B.5.33}$$
である。ここで、対応する光を観測者が観測するときの波長 \(\lambda_0\) 、時間間隔 \(\Delta t_0\) は赤方偏移によって、\(\lambda_0 = (1 + z)\lambda\) 、\(\Delta t_0 = (1 + z) \Delta t\) となるので、式(2.5.33)は
$$ \Delta N = \frac{1}{(1 + z)^3} \frac{L}{2\pi\hbar c} \lambda_0 I\left(\frac{\lambda_0}{1 + z}\right) \Delta\lambda_0 \Delta t_0 \tag{B.5.34}$$
と表される。光源からRW計量の座標距離 \(r\) にある球面の面積は \(4\pi r^2\) である(そうなるように座標距離が定義された)。したがって、観測者が単位面積、単位時間あたりに受けるエネルギーは
$$ F(\lambda_0) \Delta\lambda_0 = \frac{2\pi \hbar c/\lambda_0\cdot\Delta N }{4\pi r^2 \Delta t_0} \tag{B.5.35}$$
であるから,観測者の位置でのフラックスは、
$$ F(\lambda_0) = \frac{L\cdot I\left[\lambda_0/(1+z)\right]}{4\pi r^2 (1+z)^3} \tag{B.5.36}$$
である。
放射の全エネルギーを測る抵抗熱量計のことをボロメータ (bolometer) という。ボロメータによって測定したエネルギーは全波長で積分したフラックスに対応するので、これをボロメトリックフラックス (bolometric flux) と言い、
$$ F_{\rm bol} = \int^\infty_0 d\lambda_0 F(\lambda_0) \tag{B.5.37}$$
で与えられる。また、天体から放出される全エネルギーはボロメトリック光度に対応し、
$$ L_{\rm bol} = \int^\infty_0 d\lambda L\cdot I(\lambda) = L \tag{B.5.38}$$
である。したがって、これらの関係はよりシンプルに、
$$ F_{bol}=\frac{L_{bol}}{4\pi r^2 (1+z)^2} \tag{B.5.39}$$
となる.このボロメトリックな量を用いて,あたかも静止ユークリッド空間であるかのように天体までの距離を見積もったものを,光度距離(luminosity distance) \(d_{\rm L}\) という:
$$ d_{\rm L} \equiv \sqrt{\frac{L_{\rm bol}}{4\pi F_{\rm bol}}} = (1 + z) r \tag{B.5.40}$$
さて、フラックスを対数スケールで表したものは伝統的な等級 (magnitude) である。ボロメトリックな見かけの等級は
$$ m = -2.5 \log \left(\frac{F_{\rm bol}}{F_0 } \right) \tag{B.5.41}$$
で与えられる(\footnote B1)。ここで、
$$ F_0 = 2.52 \times 10^{-5} {\rm erg} \cdot {\rm cm}^{-2} \cdot {\rm s}^{-1} \tag{B.5.42}$$
は等級がゼロに対応するフラックスである。また、ある天体が10pcの距離にあったとしたときの見かけの等級は絶対等級と呼び、ボロメトリックの場合
$$ M = -2.5 \log \left(\frac{L_{\rm bol}}{ 4\pi (10{\rm pc})^2 F_0} \right) \tag{B.5.43}$$
で与えられる。これらの等級を用いれば、光度距離は
$$ d_{\rm L} = 10^{1 + 0.2(m - M)} {\rm pc} \tag{B.5.44}$$
となる。したがって \(m-M\) は光度距離と一対一の関係にあるため、これを距離指数 (distance modulus) と呼び、以下のような式で与えられる:
$$ m - M \hskip 1em \left\{
\begin{array}{ll} = & 5\log\left(\frac{d_{\rm L}}{10{\rm pc}}\right) \\
= & 5 \log\left(\frac{d_{\rm L}}{{\rm pc}}\right) - 5 \\
= & 5 \log\left(\frac{d_{\rm L}}{{\rm Mpc}}\right) + 25\\
= & 5 \log\left(\frac{r}{{\rm Mpc}}\right) + 5 \log(1 + z) + 25
\end{array} \right. \tag{B.5.45}$$
全光度を測定しない、あるいはできない場合は波長の範囲を限定した観測となり、上のようなシンプルな式には補正が必要である。これをK-補正 (K-correction) と呼ぶ。あるバンドBandに限定した観測を行うことを考えてみる。このときのフラックスは
$$ F_{\rm Band} = \int_{\rm Band} F(\lambda_0) d\lambda_0 =
\frac{L \int_{\rm Band} I[\lambda_0/(1+z)]d\lambda_0}{4\pi r^2 (1+z)^3} \tag{B.5.46}$$
で与えられる。この天体が10pcにあるとしたときのフラックスは
$$ F_{\rm{Band,10}} =
\frac{L \int_{\rm Band} I(\lambda_0) d\lambda_0}
{4\pi (\rm 10pc)^2} \tag{B.5.47}$$
であるから、このバンドでの距離指数は、
$$ m_{\rm Band} - M_{\rm Band} = 5 \log\left(\frac{d_{\rm L}}{10{\rm pc}}\right) - K(z) \tag{B.5.48}$$
となる。ここで、\(K(z)\) がK-補正であり、
$$ K(z) = 2.5\, {\rm log} \left(
\frac{\int_{\rm Band} I[\lambda_0/(1+z)]d\lambda_0/(1+z)}
{\int_{\rm Band} I(\lambda_0) d \lambda_0} \right) \tag{B.5.49}$$
で与えられる。これは天体のスペクトル分布 \(I(\lambda)\) を知ることにより計算できる。
ハッブル図(Hubble Plot)
ハッブル則 (Hubble's Law) は、銀河の後退速度 \(v\) と天体までの距離 \(d\) についての関係式 \(v = H_0 d\) で与えられた。ここで、後退速度と言っているものは赤方偏移を非相対論的後退速度によるドップラー効果と解釈した場合のものであり、観測量としては赤方偏移に光速をかけた \(v = cz\) で実際には与えられるものである。また、距離 \(d\) は絶対光度の推定のもとに見かけの光度を用いて見積もったものであるから、光度距離 \(d_{\rm L}\) に他ならない。また、ハッブル則は赤方偏移の小さな \(z\ll 1\) の観測によって求められたものである。したがって、ハッブル則は
$$ d_{\rm L} = \frac{cz}{H_0} + {\cal O}(z^2) \tag{B.6.50}$$
と表すことができる。
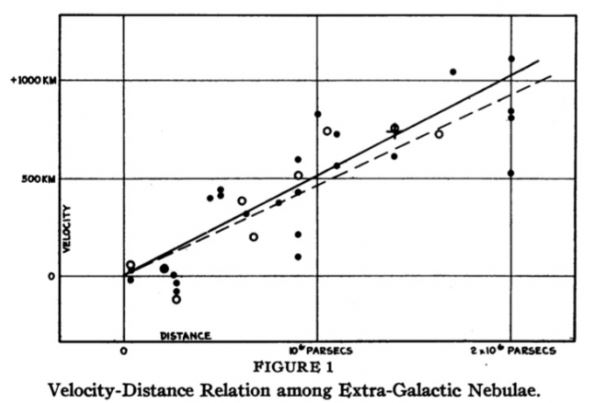
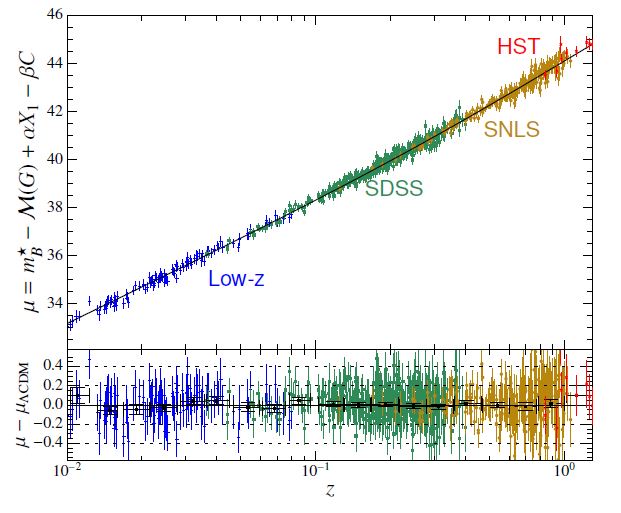
ハッブル・プロット:左は1929年にハッブルが発表した図[Hubbleの1929年論文] 、右は超新星Ia型を使って測定した最近の図:上のパネルがハッブル・プロットで下は宇宙論モデルとのずれを示す[Betoule他の2014年の論文]
これをRW計量のもとで導いてみよう。そのためには、式(2.5.40)を \(z\) でテイラー展開すればよい。そのためにまず、スケール因子 \(a(t)\) を現在時刻 \(t_0\) のまわりでテイラー展開する:
$$ a(t) = 1 + \dot{a}(t_0)(t - t_0) + \frac12 \ddot{a}(t_0) (t - t_0)^2 + {\cal O}(t-t_0)^3 \tag{B.6.51}$$
ここで,ドットは時間微分を表す。すると、赤方偏移の展開は、
$$ z = \frac{1}{a(t)} - 1 = \dot{a}(t_0) (t_0 - t) + \left(\dot{a}^2(t_0) - \frac12 \ddot{a}(t_0)\right) (t_0 - t)^2 + {\cal O}(t_0 - t)^3 \tag{B.6.52}$$
である。一方、座標距離 \(r\) の展開は式(2.4.26)より求められ、2次まででは曲率 \(K\) によらず、
$$ r = c\left[t_0 - t + \frac12 \dot{a}(t_0) (t_0 - t)^2 + {\cal O}(t-t_0)^3\right] \tag{B.6.53}$$
となる。したがって、式(2.5.40)、(2.6.52)、(2.6.53)を使えば光度距離を赤方偏移で展開した式が得られる:
$$ d_{\rm L} = \frac{c}{\dot{a}(t_0)} \left[ z + \frac12 \left(1 + \frac{\ddot{a}(t_0)}{\dot{a}^2(t_0)}\right) z^2 + {\cal O}(z^3) \right] \tag{B.6.54}$$
これを式(2.6.50)と比べれば、ハッブル定数はRW計量においてスケール因子の時間微分
$$ H_0 = \dot{a}(t_0) \tag{B.6.55}$$
であることがわかる。また、赤方偏移の2次の項の存在は赤方偏移の大きいところでハッブル則が線形からずれることを示している。減速パラメータ
$$ q_0 \equiv - \frac{\ddot{a}(t_0)}{\dot{a}^2(t_0)} \tag{B.6.56}$$
を導入すれば、線形関係からの2次の補正が特徴づけられる。すなわち、光度距離の展開は、
$$ d_{\rm L} = \frac{c}{H_0} \left[ z + \frac12 (1 - q_0) z^2 + {\cal O}(z^3) \right] \tag{B.6.57}$$
と書ける。
見かけのサイズ(Apparent Size)
次に、天体の見かけのサイズがRW計量のもとでどう見えるか調べてみる。天体の視線方向に垂直なサイズを \(l\) とし、見かけの角度を \(\Delta\theta\) とする。ここで角度 \(\Delta\theta\) は十分小さいものとする。すると、静止ユークリッド空間では、
$$ \Delta\theta = \frac{l}{r} \tag{B.7.58}$$
が成り立つが、RW計量ではこれに変更が加わる。RW計量において、\(dr = d\phi = 0\) とおくことにより、視線に垂直な方向に実距離 \(l\) だけ離れた2点 A、Bを考えれば、
$$ l = \int_A^B cdt = a r \int_A^B d\theta = a r \Delta\theta = \frac{r}{1+z}\Delta\theta \tag{B.7.59}$$
となる。つまり、見かけの角度は
$$ \Delta\theta = \frac{(1+z) l}{r} \tag{B.7.60}$$
である。
ここで、あたかも静止ユークリッド空間であるかのようにして見かけの角度から見積もった距離
$$ d_{\rm A} = \frac{l}{\Delta\theta} = \frac{r}{1+z} \tag{B.7.61}$$
を角径距離(angular diameter distance)という。光度距離との間には
$$ d_{\rm A} = \frac{d_{\rm L}}{(1+z)^2} \tag{B.7.62}$$
の関係があり、赤方偏移によるテイラー展開は
$$ d_{\rm A} = \frac{c}{H_0} \left[ z - \frac12 (3 + q_0) z^2 + {\cal O}(z^3) \right] \tag{B.7.63}$$
となる。
表面輝度(Surface Brightness)
広がった天体の像において、単位立体角あたりに検出される光のエネルギー量 \(B\) を表面輝度 (surface brightness) という.天体の像において、見かけの角度 \(\Delta\theta\) を直径とする微小な円をとり、対応する天体の部分の視線に垂直な方向の実際の直径を \(l\) とする。すると、この部分のボロメトリックフラックスについて、
$$ B = \frac{F_{\rm bol}}{\pi (\Delta\theta/2)^2} = \frac{L_{\rm bol}}{\pi^2 l^2} (1 + z)^{-4} \tag{B.8.64}$$
となる。ここで特徴的なことは、表面輝度は座標距離 \(r\) にはよらないことである。まず、赤方偏移の小さい場合には、表面輝度は距離によらない。遠くの天体は全体の明るさは暗くなるが、その分小さく見えるので輝度にすれば変化がない。一方,赤方偏移が大きいところでは \((1+z)^{-4}\) の依存性を持つ。天体に固有の量 \(L_{\rm bol}\) 、\(l\) を知ることのできるものがあれば、この \(z\) 依存性は膨張宇宙が必ず満たさなければならないものである。したがって、これは膨張宇宙論そのものテストになる。
銀河の計数(Galaxy Count)
共動体積あたりの銀河の数がもし一定であるとすると、銀河の数が共動体積の指標になる。遠くの宇宙で共動体積がどう変化するかは宇宙の曲率や膨張速度を反映しているので、これらを決める方法になると考えられる。座標距離 \(r\) よりも内側にある銀河の総数を \(N(r)\) とすると、共動体積あたりの銀河の数 \(n_0\) が一定の場合、
$$ N(r) = n_0 \int_{r'\le r} d^3 r' \sqrt(\gamma)
= 4 \pi n_0 \int_{0}^{r} \frac{r^2 dr}{\sqrt(1-Kr^2)} \tag{B.9.65}$$
となる。このテイラー展開は、
$$ N(z) = 4 \pi n_0 \left(\frac{cz}{H_0}\right)^3 \left[1 - \frac32 (1 + q_0) z + {\cal O}(z^2)\right] \tag{B.9.66}$$
となり、比較的近傍の宇宙で \(N(z)\) の \(z\) 依存を観測することにより減速パラメータ \(q_0\) が原理的に求められる。より遠くの宇宙を観測すればスケール因子の振舞いがさらに詳細にわかると考えられる。
現実には銀河の数は一定でないであろうことに加えて、遠くの暗い銀河は観測にかからないので、そうでなくても数が減る。そこで上の方法を実際に用いるにはどのような明るさの銀河が単位共動体積あたりいくつ存在するかをあらかじめ見積もっておく必要がある。観測するバンド、感度によって、どのようなスペクトルを持つ銀河を観測できるかが決まるので、銀河のスペクトルの進化と数密度変化の知識が必要である。だが、銀河の形成、進化がまだ理論的にはっきりとは明らかになっていないため、これらを正しく見積もるのは実際には容易なことではない。
一章の文献
Wikipedia https://en.wikipedia.org/wiki/Friedmann–Lemaître–Robertson–Walker_metric
Hubble, E. (1929). "A relation between distance and radial velocity among extra-galactic nebulae". Proceedings of the National Academy of Sciences. 15 (3): 168–73.
"Improved cosmological constraints from a joint analysis of the SDSS-II and SNLS supernova samples", M. Betoule et al., Astron. Astrophys. 568 (2014) A12.